Solving a Killer Sudoku
I work for IBM and I am based at the Hursley Laboratory near Southampton, UK. In addition to the large campus including an 18th century mansion, a sunken garden and many sporting grounds, we have a Club House. For Christmas 2018, the Hursley Club sent a newsletter including a few puzzles.
I initially did not know about it and first heard of it when colleagues were discussing one of the puzzles that still stood unsolved a few weeks later. It looked like a type of Sudoku but it did not contain any initial numbers but instead had areas with larger numbers.
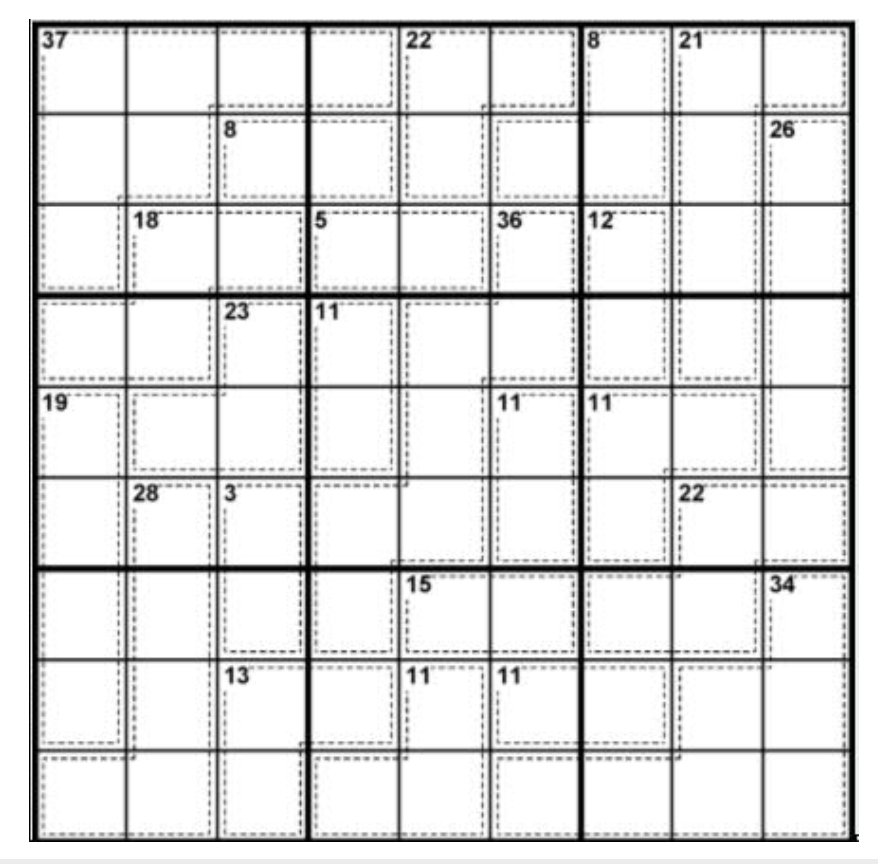
After a quick search, it turns out this puzzle is called a Killer Sudoku. While I often play Sudokus, I was not aware of this variant. As colleagues made no progress on it, it sparked my interest and I decided to attempt solving it.
If you want to try solve it yourself, stop reading here as I’ll detail my method below.
Getting started
Wikipedia has a Killer Sudoku page detailling the specifics of this type of puzzles, and I’ll reuse its terminology.
By convention, most grids do not include duplicate numbers in a single cage. I assumed this was the case for this puzzle.
I first started naming each cage and finding all the possible number combinations for all of them.
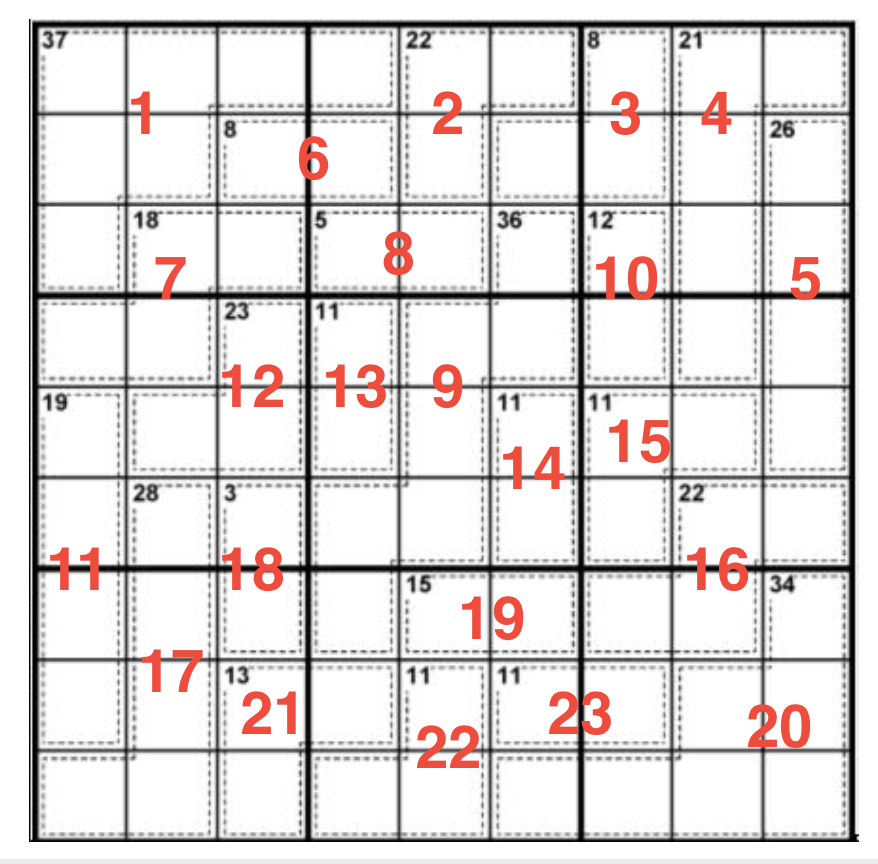
I could have used an existing combination table but decided to write some Python. I don’t have the code anymore but I hda printed its output:
1: 3 matches [(1,2,4,6,7,8,9), (1,3,4,5,7,8,9), (2,3,4,5,6,8,9)] excludes [] all [4,8,9]
2: 2 matches [(5,8,9), (6,7,9)] excludes [1,2,3,4] all [9]
3: 2 matches [(1,2,5), (1,3,4)] excludes [6,7,8,9] all [1]
4: 8 matches [(1,2,3,6,9), (1,2,3,7,8), (1,2,4,5,9), (1,2,4,6,8), (1,2,5,6,7), (1,3,4,5,8), (1,3,4,6,7), (2,3,4,5,7)] excludes [] all []
5: 5 matches [(2,7,8,9), (3,6,8,9), (4,5,8,9), (4,6,7,9), (5,6,7,8)] excludes [1] all []
6: 3 matches [(1,7), (2,6), (3,5)] excludes [4,8,9] all []
7: 11 matches [(1,2,6,9), (1,2,7,8), (1,3,5,9), (1,3,6,8), (1,4,5,8), (1,4,6,7), (2,3,4,9), (2,3,5,8), (2,3,6,7), (2,4,5,7), (3,4,5,6)] excludes [] all []
8: 2 matches [(1,4), (2,3)] excludes [5,6,7,8,9] all []
9: 4 matches [(1,2,3,6,7,8,9), (1,2,4,5,7,8,9), (1,3,4,5,6,8,9), (2,3,4,5,6,7,9)] excludes [] all [9]
10: 3 matches [(3,9), (4,8), (5,7)] excludes [1,2,6] all []
11: 11 matches [(1,2,7,9), (1,3,6,9), (1,3,7,8), (1,4,5,9), (1,4,6,8), (1,5,6,7), (2,3,5,9), (2,3,6,8), (2,4,5,8), (2,4,6,7), (3,4,5,7)] excludes [] all []
12: 1 match [(6,8,9)] excludes [1,2,3,4,5,7] all [6,8,9]
13: 4 matches [(2,9), (3,8), (4,7), (5,6)] excludes [1] all []
14: 4 matches [(2,9), (3,8), (4,7), (5,6)] excludes [1] all []
15: 5 matches [(1,2,8), (1,3,7), (1,4,6), (2,3,6), (2,4,5)] excludes [9] all []
16: 11 matches [(1,4,8,9), (1,5,7,9), (1,6,7,8), (2,3,8,9), (2,4,7,9), (2,5,6,9), (2,5,7,8), (3,4,7,8), (3,5,6,8), (4,5,6,7)] excludes [] all []
17: 9 matches [(1,3,7,8,9), (1,4,6,8,9), (1,5,6,7,9), (2,3,6,8,9), (2,4,5,8,9), (2,4,6,7,9), (2,5,6,7,8), (3,4,5,7,9), (3,4,6,7,8)] excludes [] all []
18: 1 match [(1,2)] excludes [3,4,5,6,7,8,9] all [1,2]
19: 2 matches [(6,9), (7,8)] exckudes [1,2,3,4,5] all []
20: 4 matches [(1,2,3,4,7,8,9), (1,2,3,5,6,8,9), (1,2,4,5,6,7,9), (1,3,4,5,6,7,8)] excludes [] all [1]
21: 7 matches [(1,3,9), (1,4,8), (1,5,7), (2,3,8), (2,4,7), (2,5,6), (3,4,6)] excludes [] all []
22: 5 matches [(1,2,8), (1,3,7), (1,4,6), (2,3,6), (2,4,5)] excludes [9] all []
23: 4 matches [(2,9), (3,8), (4,7), (5,6)] excludes [1] all []
For each cage, there’s first the number of possible combinations, followed by each combinations. Then excludes denotes numbers that don’t appear in any combinations and finally all denotes numbers that appear in all combinations.
Placing all the possible numbers in each cell, we have:
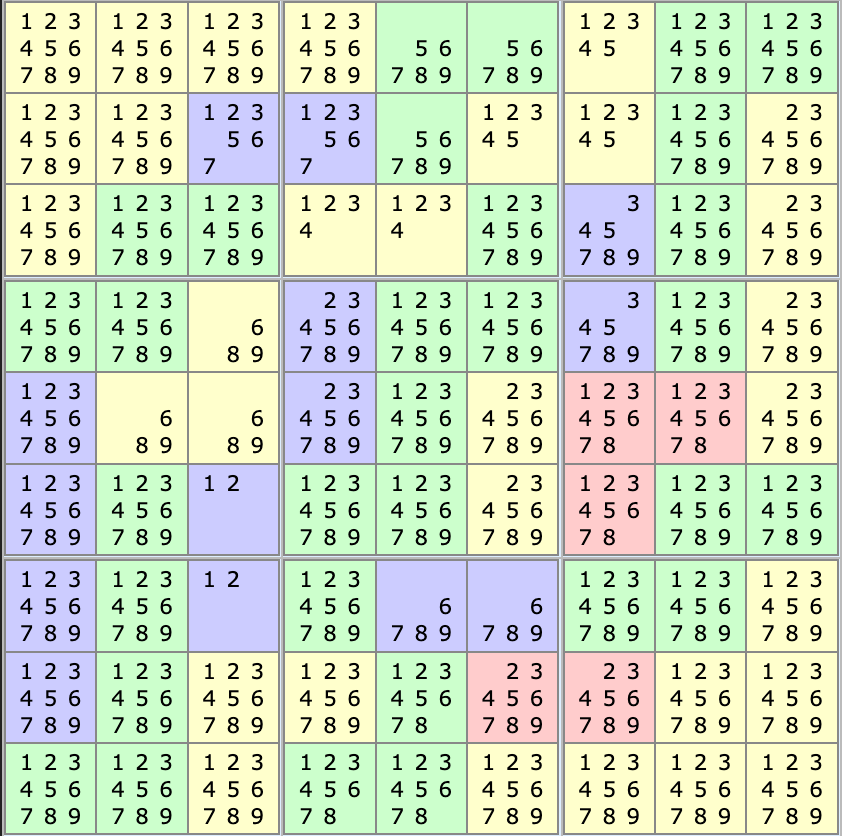
Hopeful Beginnings
Immediately some simplifications appear:
-
on the 3rd column,
1and2have to be in cage 18, so they can’t be used in any other cells in this column. Also removing1and2from the left cell of cage 6 makes it impossible to have7or6in the right cell. A further simplication, slightly less obvious, can then be made in cage 21, as the cells in column 3 can’t contain1nor2, the 3rd cell can’t be5,7,8or9. -
in the middle box on the left,
6,8and9have to be in cage 12, so they can’t be in any other cells in this box. -
in the middle box on the top,
9must be contained in cage 2, so we can remove9from the other cells in this box.
After these initial simplifications, we have:
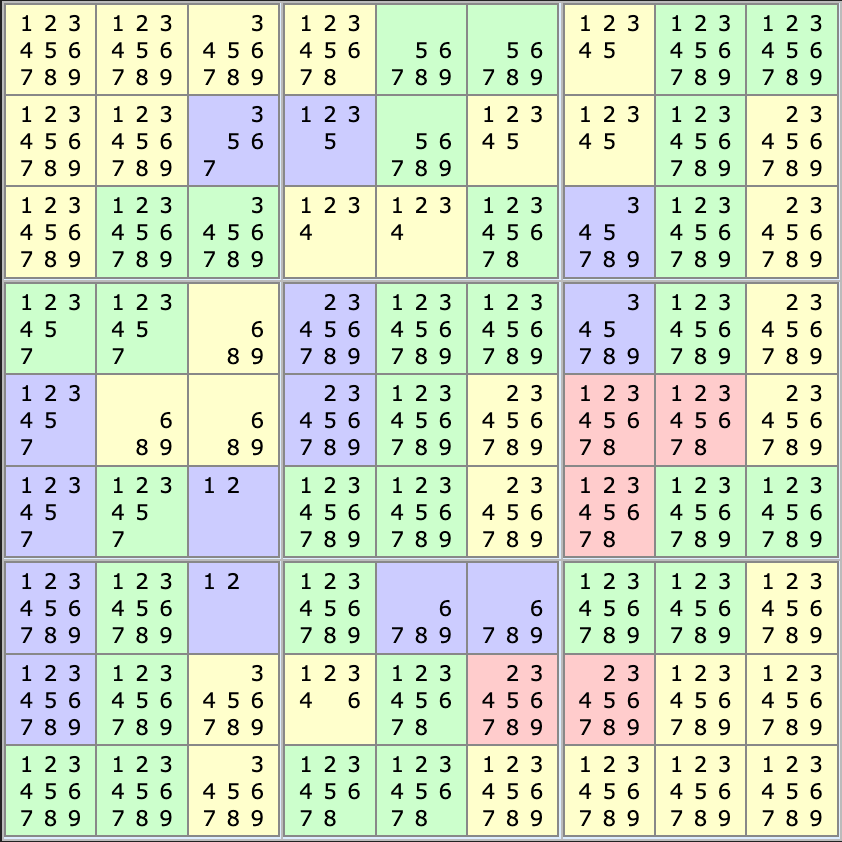
Hitting the Wall
At this point, the grunt work started and I spent a while starring at the grid trying to get a foothold. I first was attracted by the area around cages 12 and 18 as both of these have a single possible combination but I made no progress. I spent a couple of hours blocked at this stage, unable to find another simplification.
I guess most people reached this stage and quit here. I actually tried a few Killer Sudoku solvers and none of them were able to make progress either! At that time, I was pretty busy so I left my notes on my desk, hoping to take another look later.
Symmetry for the Win
A few months later, I just happened to look at notes left on my desks and stumbled on that Killer Sudoku grid. Looking at the grid again, I realized it has a diagonal symmetry. I then remembered it was indeed mentioned in the Wikipedia page, that some puzzles, could have such a symmetry. Immediately this attracted my attention to the center of the grid where the center of symmetry lies. Maybe it was finally time to solve this puzzle!
In the center, we have this:
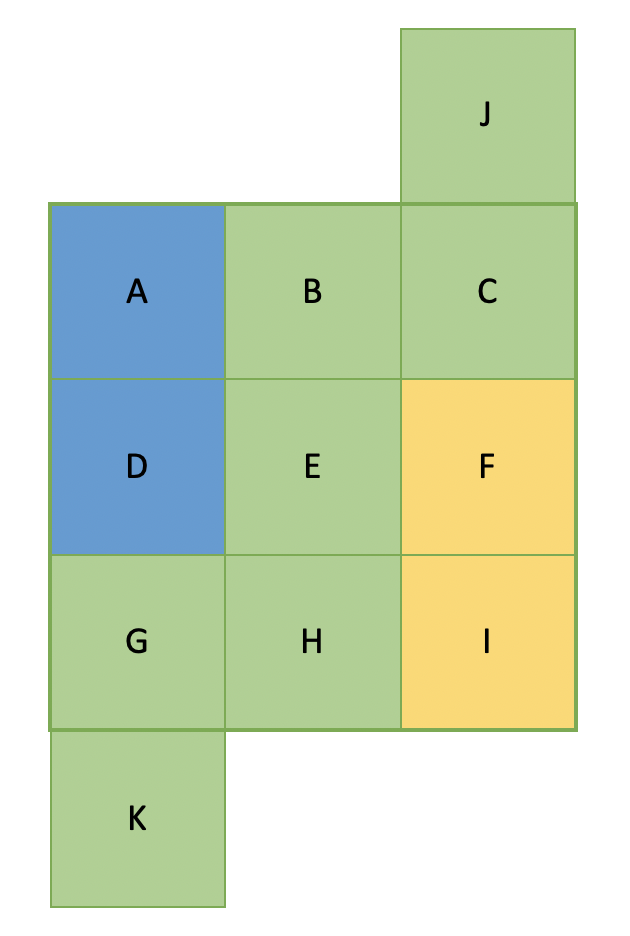
We can make a few interesting deductions just from that shape!
The box contains cage 13 and 14 completely as well as 5 cells (B, C, E, G, H) from cage 9. We can deduce the sum of these 5 cells to be equal to:
Sum(box) - Sum(Cage 13) + Sum(Cage 14) = 45 - 11 - 11 = 23
Let’s see how many combinations of 5 numbers can add up to 23:
1,2,3,8,91,2,4,7,91,2,5,6,91,2,5,7,81,3,4,6,91,3,4,7,81,3,5,6,81,4,5,6,7
Hmm, 8 options is still a lot … but we can make a few further deductions.
Because cage 9 total sum is 36, we can also deduce the remaining 2 cells (J, K) add up to 13 and have the following combinations:
4,95,86,7
On the other hand, we already know that both cage 13 and 14 are made of the following combinations:
2,93,84,75,6
And we need to be able to pick 2 of these to satisfy both cage 13 and 14.
At this point, we can rule out a few of the combinations that makes 23.
1,2,5,6,9is impossible as containing5,6and9prevents picking any combination for cells J and K1,2,5,7,8is impossible as containing2,5and8prevents picking 2 combinations for cage 13 and 141,3,4,6,9is impossible as containing4,6and9prevents picking 2 combinations for cage 13 and 141,3,4,7,8is impossible as containing4,7and8prevents picking any combination for cells J and K1,4,5,6,7is impossible as containing4,5and6prevents picking any combination for cells J and K
We are left with 3 possible options:
1,2,3,8,91,2,4,7,91,3,5,6,8
It’s a bit less obvious but 2 of these also lead to contradictions:
1,2,3,8,9is impossible. It would force cage 13 and 14 to be made of4,7and5,6. However it also forces J and K to be either6or7. Both of these can’t be satisfied.1,2,4,7,9is impossible. It would force cage 13 and 14 to be made of3,8and5,6. However it also forces J and K to be either5or8. Both of these can’t be satisfied.
We are now left with one possible option for cells B, C, E, G, H: 1,3,5,6,8. Cells J and K have to be 4 and 9, and cages 13 and 14 are made of 2,9 and 4,7. Putting everything in our grid, we obtain:
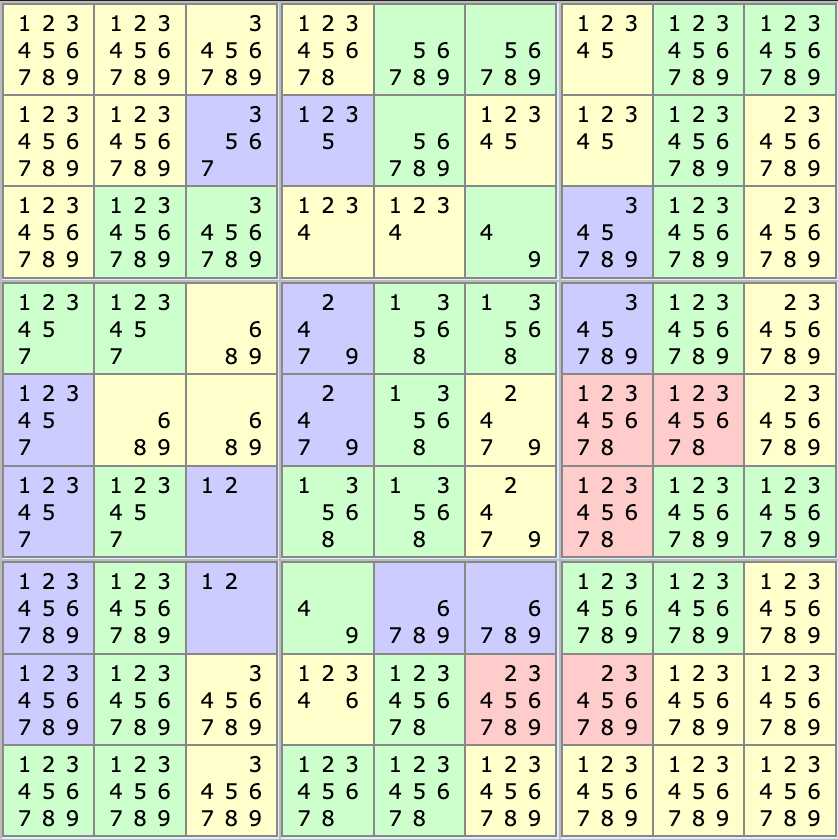
Placing the First Numbers
Now that we’ve simplified the center a bit, we can try again to apply common strategies.
At first glance, we can see cells J and K create some “naked pairs” which is a very common Sudoku technique. So we can remove 4 and 9 from cells in row 3 and 7 not having both of these numbers. Removing 4 from the rightmost cell in cage 8, also removes 1 in the leftmost cell. Similarly, 6 can be removed from the leftmost cell in cage 19.
Looking at the middle box on the top row, we know all combinations of cage 2 contain a 9. So we can remove the 9 from the top cell of cage 9, allowing us to place our first two numbers on the grid!
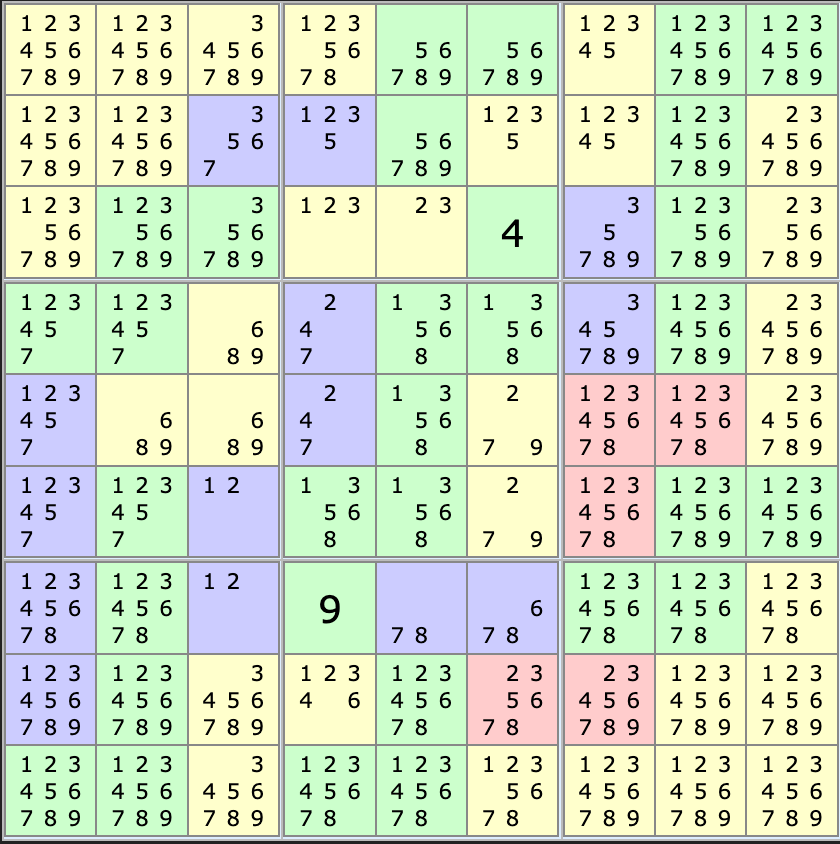
Because of the 9 we just placed, cage 13 must be the 4,7 combination, so we can remove 2 from it. That forces cage 14 to be 2,9. We can now remove all other 4s and 7s from column 4 and all other 2s and 9s from column 6.
We can simplify the middle box on the top row, as the outer cells on the middle row and the left and middle cells on the bottom row form a “naked quad” of 1,2,3,5, so we can remove these numbers from the other cells in this box.
On the 2nd row, we see that 5 needs to appear in the middle box, so we can remove it from the rest of the row.
Still in the middle box on the top row, cage 2 and 8 add up to 27. We already have a 4 placed, so the 3 remaining cells must add to 14. As it must contain either 6 or 8, the rightmost cell of cage 6 cannot contain 2. This forces 2 to be in the middle box for row 3, so we can remove it from the rest of the row.
Checking the grid again, we are now at:
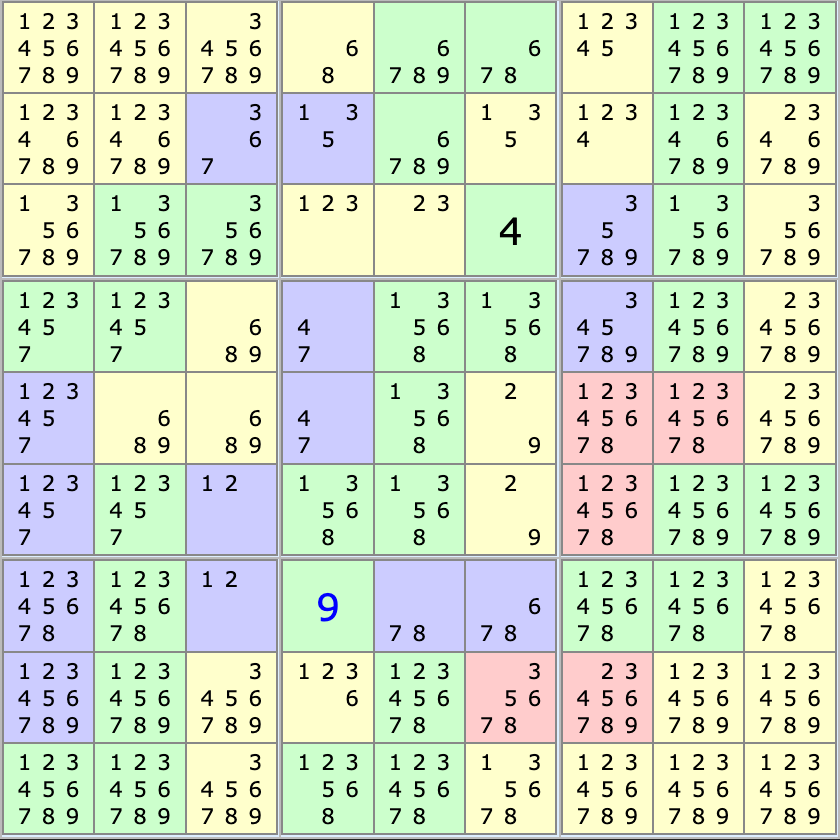
Putting it together
At this point, I started to read into known strategies to solve this type of Sudokus. This part can feel like grunt work as progress is relatively slow but from that point I was never not blocked again. I am not going to explain all the remaining steps to finish the grid as this would take far too long and be relatively boring. But let’s see how the next couple of simplifications work as I found them pretty interesting. It’s worth noting here that without knowing about some existing strategies, I feel like some of the next steps can be relatively tricky to find.
Looking at the middle box on the bottom row, it is made of cage 19 and 22. The sum of these 2 cages is 24 and we already have a 9 so the 3 remaining cells must add to 10. We allows us to remove 8 from the rightmost cell in the middle row and 7 and 8 from the rightmost cell in the bottom row of this box.
Looking at the 4 leftmost columns, we know their sum must be 180 (4 x 45). If we add the value of all cages fully in this area (cage 1,6,7,11,12,13,17,18,21), we get 160. This area also contains a 9, so the sum of the 3 remaining cells in this area must be 11. Because these cells can’t contain a 4, they can’t contain 5s either.
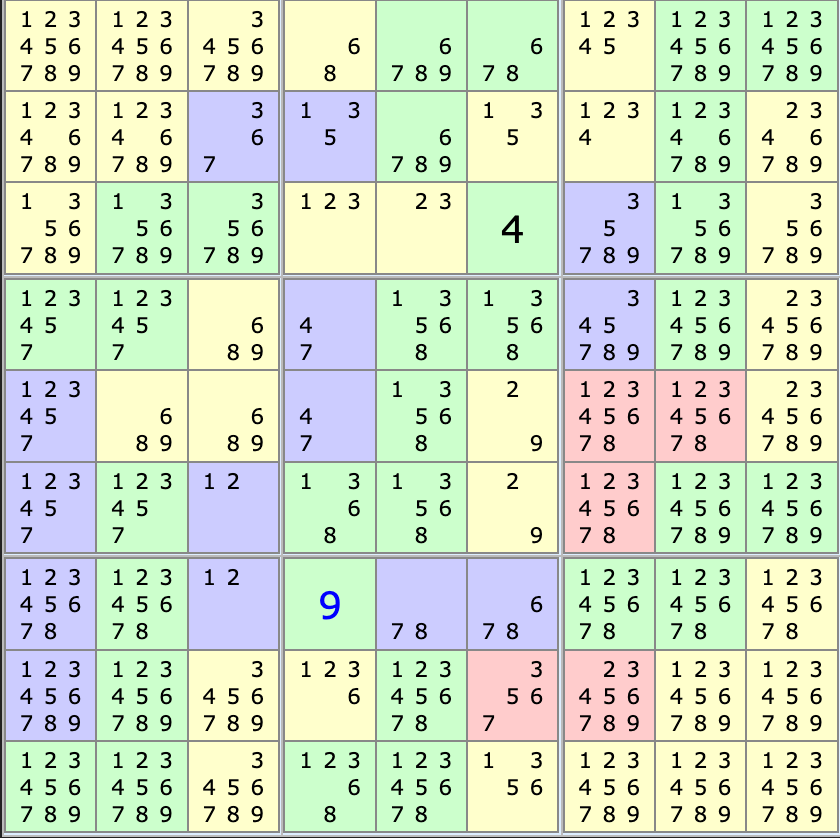
Finishing the grid
As I made more simplifications, it started becoming easier and I was able to progress faster, until I completed the grid!
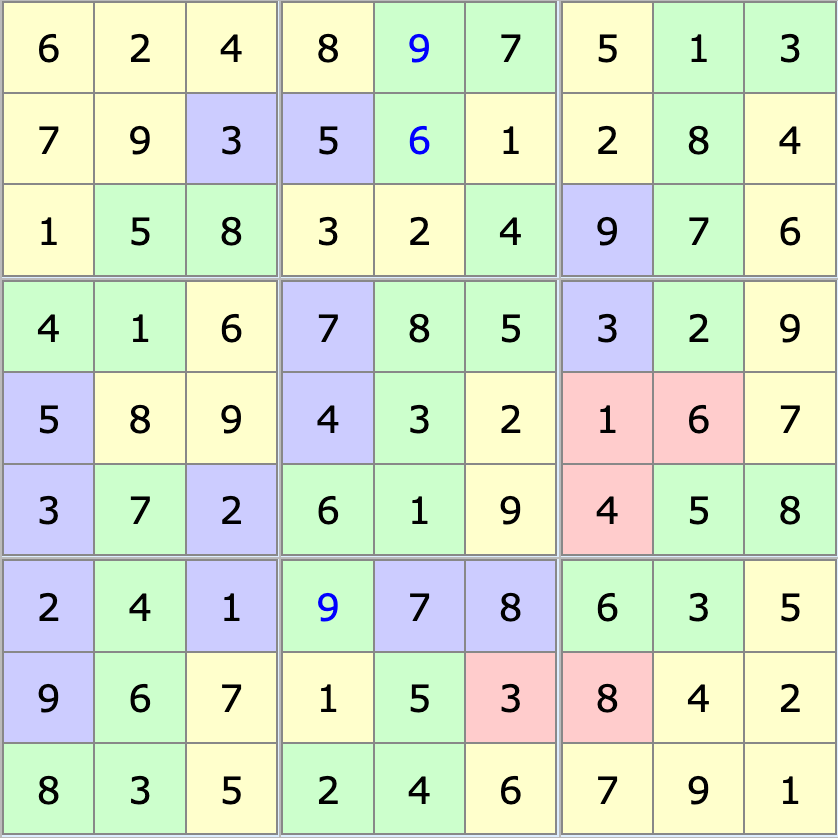
In total, I probably spent around 8 hours to complete the grid. It took me about half of that to place the first numbers. I then finished the grid in short sessions over a few days.
I wrote most of this post back in fall 2019 when I did it but never got around to publishing it. The main reason I decided to finally publish it is because none of the solvers I tried could solve it. Most of them are able to do it once the simplifications described in Symmetry for the Win are done. So I am wondering how this strategy could be implemented and whether it is applicable to many grids?
Since then, I have not attempted another grid. While I enjoyed the experience, to me the best part was finding the breakthrough and getting started. I found the second part, applying all the simplifications, a bit too long. That said, I am pretty sure I will try another grid at some point!
References
I used https://www.sudokuwiki.org/killersudoku.htm for most images in this post. I also used it to learn about advanced solving strategies.